satori/sakuya
1
0
Fork 0
Code Issues Pull Requests Packages Projects Releases Wiki Activity

整理桌面

Browse Source
This commit is contained in:
satori
2022-04-10 00:37:53 +08:00
parent 82e3f2623f
commit e25c8bb318
728 changed files with 986384 additions and 16 deletions
Download Patch File Download Diff File Expand all files Collapse all files

38
node_modules/neataptic/mkdocs/templates/docs/methods/activation.md generated vendored Normal file
View File

@@ -0,0 +1,38 @@
description: List of activation functions in Neataptic
authors: Thomas Wagenaar
keywords: activation function, squash, logistic sigmoid, neuron
Activation functions determine what activation value neurons should get. Depending on your network's environment, choosing a suitable activation function can have a positive impact on the learning ability of the network.
### Methods
Name | Graph | Equation | Derivative
---- | ----- | -------- | ----------
LOGISTIC | <img src="http://imgur.com/LR7dIMm.png" width="120px"/> | $ f(x) = \frac{1}{1+e^{-x}} $ | $ f'(x) = f(x)(1 - f(x)) $
TANH | <img src="http://imgur.com/8lrWuwU.png" width="120px"/> | $ f(x) = tanh(x) = \frac{2}{1+e^{-2x}} - 1 $ | $ f'(x) = 1 - f(x)^2 $
RELU | <img src="http://imgur.com/M2FozQu.png" width="120px"/> | $ f(x) = \begin{cases} 0 & \text{if} & x \lt 0 \\\ x & \text{if} & x \ge 0 \end{cases} $ | $ f'(x) = \begin{cases} 0 & \text{if} & x \lt 0 \\\ 1 & \text{if} & x \ge 0 \end{cases} $
IDENTITY | <img src="http://imgur.com/3cJ1QTQ.png" width="120px"/> | $ f(x) = x $ | $ f'(x) = 1 $
STEP | <img src="http://imgur.com/S5qZbVY.png" width="120px"/> |$ f(x) = \begin{cases} 0 & \text{if} & x \lt 0 \\\ 1 & \text{if} & x \ge 0 \end{cases} $| $ f'(x) = \begin{cases} 0 & \text{if} & x \neq 0 \\\ ? & \text{if} & x = 0 \end{cases} $
SOFTSIGN | <img src="http://imgur.com/8bdal1j.png" width="120px"/> | $ f(x) = \frac{x}{1+\left\lvert x \right\rvert} $ | $ f'(x) = \frac{x}{{(1+\left\lvert x \right\rvert)}^2} $
SINUSOID | <img src="http://imgur.com/IbxYwL0.png" width="120px"/> | $ f(x) = sin(x) $ | $ f'(x) = cos(x) $
GAUSSIAN | <img src="http://imgur.com/aJDCbPI.png" width="120px"/> | $ f(x) = e^{-x^2} $ | $ f'(x) = -2xe^{-x^2} $
BENT_IDENTITY | <img src="http://imgur.com/m0RGEDV.png" width="120px"/> | $ f(x) = \frac{\sqrt{x^2+1} - 1}{2} + x$ | $ f'(x) = \frac{ x }{2\sqrt{x^2+1}} + 1 $
BIPOLAR | <img src="http://imgur.com/gSiH8hU.png" width="120px"/> | $ f(x) = \begin{cases} -1 & \text{if} & x \le 0 \\\ 1 & \text{if} & x \gt 0 \end{cases} $ | $ f'(x) = 0 $
BIPOLAR_SIGMOID | <img src="http://imgur.com/rqXYBaH.png" width="120px"/> | $ f(x) = \frac{2}{1+e^{-x}} - 1$ | $f'(x) = \frac{(1 + f(x))(1 - f(x))}{2} $
HARD_TANH | <img src="http://imgur.com/WNqyjdK.png" width="120px"/> | $ f(x) = \text{max}(-1, \text{min}(1, x)) $ | $ f'(x) = \begin{cases} 1 & \text{if} & x \gt -1 & \text{and} & x \lt 1 \\\ 0 & \text{if} & x \le -1 & \text{or} & x \ge 1 \end{cases} $
ABSOLUTE<sup>1</sup> | <img src="http://imgur.com/SBs32OI.png" width="120px"/> | $ f(x) = \left\lvert x \right\rvert $ | $ f'(x) = \begin{cases} -1 & \text{if} & x \lt 0 \\\ 1 & \text{if} & x \ge 0 \end{cases} $
SELU | <img src="http://i.imgur.com/BCSi7Lu.png" width="120px"/> | $ f(x) = \lambda \begin{cases} x & \text{if} & x \gt 0 \\\ \alpha e^x - \alpha & \text{if} & x \le 0 \end{cases} $ | $ f'(x) = \begin{cases} \lambda & \text{if} & x \gt 0 \\\ \alpha e^x & \text{if} & x \le 0 \end{cases} $
INVERSE | <img src="http://imgur.com/n5RiG7N.png" width="120px"/> | $ f(x) = 1 - x $ | $ f'(x) = -1 $
<sup>1</sup> avoid using this activation function on a node with a selfconnection
### Usage
By default, a neuron uses a [Logistic Sigmoid](http://en.wikipedia.org/wiki/Logistic_function) as its squashing/activation function. You can change that property the following way:
```javascript
var A = new Node();
A.squash = methods.activation.<ACTIVATION_FUNCTION>;
// eg.
A.squash = methods.activation.SINUSOID;
```

40
node_modules/neataptic/mkdocs/templates/docs/methods/cost.md generated vendored Normal file
View File

@@ -0,0 +1,40 @@
description: List of cost functions in Neataptic
authors: Thomas Wagenaar
keywords: cost function, loss function, mse, cross entropy, optimize
[Cost functions](https://en.wikipedia.org/wiki/Loss_functions_for_classification)
play an important role in neural networks. They give neural networks an indication
of 'how wrong' they are; a.k.a. how far they are from the desired output. But
also in fitness functions, cost functions play an important role.
### Methods
At the moment, there are 7 built-in mutation methods (all for networks):
Name | Function |
---- | ------ |
[methods.cost.CROSS_ENTROPY](http://neuralnetworksanddeeplearning.com/chap3.html#the_cross-entropy_cost_function) | ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/106c195cc961bd026ad949ad5ff89f3cde845e2c)
[methods.cost.MSE](https://en.wikipedia.org/wiki/Mean_squared_error) | ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/67b9ac7353c6a2710e35180238efe54faf4d9c15)
[methods.cost.BINARY](https://link.springer.com/referenceworkentry/10.1007%2F978-0-387-30164-8_884) | ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa1123a619eb4566439c92655d3f6331aa69c1d1)
[methods.cost.MAE](https://en.wikipedia.org/wiki/Mean_absolute_error) | ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef87b78a9af65e308cf4aa9acf6f203efbdeded)
[methods.cost.MAPE](https://en.wikipedia.org/wiki/Mean_absolute_percentage_error) | ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2557e2cbee5f1cbf3c9b474878df86d1e74189a)
[methods.cost.MSLE](none) | none
[methods.cost.HINGE](https://en.wikipedia.org/wiki/Hinge_loss) | ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5f42d461f1a28b27438e8f1641e042ff2e40102)
### Usage
Before experimenting with any of the loss functions, note that not every loss
function might 'work' for your network. Some networks have nodes with activation
functions that can have negative values; this will create some weird error values
with some cost methods. So if you don't know what you're doing: stick to any of
the first three cost methods!
```javascript
myNetwork.train(trainingData, {
log: 1,
iterations: 500,
error: 0.03,
rate: 0.05,
cost: methods.cost.METHOD
});
```

14
node_modules/neataptic/mkdocs/templates/docs/methods/gating.md generated vendored Normal file
View File

@@ -0,0 +1,14 @@
description: List of gating methods in Neataptic
authors: Thomas Wagenaar
keywords: gating, recurrent, LSTM, neuron, activation
Gating is quite the interesting: it makes the weights in networks more dynamic,
by adapting them to their gating node. Read more about it [here](https://en.wikipedia.org/wiki/Synaptic_gating).
For specific implementation of gating, check out the [Node](../architecture/node.md),
[Group](../architecture/group.md) and [Network](../architecture/network.md) wikis!
There are 3 gating methods:
* **methods.gating.OUTPUT** every node in the gating group will gate (at least) 1 node in the emitting group and all its connections to the other, receiving group
* **methods.gating.INPUT** every node in the gating group will gate (at least) 1 node in the receiving group and all its connections from the other, emitting group
* **methods.gating.SELF** every node in the gating group will gate (at least) 1 self connection in the emitting/receiving group

10
node_modules/neataptic/mkdocs/templates/docs/methods/methods.md generated vendored Normal file
View File

@@ -0,0 +1,10 @@
There are **a lot** of different methods for everything in Neataptic. This allows
the complete customization of your networks and algorithms. If you feel like any
method or function should be added, feel free to create an issue or a pull request.
* [Activation](activation.md)
* [Cost](cost.md)
* [Gating](gating.md)
* [Mutation](mutation.md)
* [Regularization](regularization.md)
* [Selection](selection.md)

135
node_modules/neataptic/mkdocs/templates/docs/methods/mutation.md generated vendored Normal file
View File

@@ -0,0 +1,135 @@
description: List of mutation methods in Neataptic
authors: Thomas Wagenaar
keywords: genetic-algorithm, mutation, modify, add, substract, genome, neural-network
[Mutation](https://en.wikipedia.org/wiki/Mutation_(genetic_algorithm)) is an important aspect of genetic algorithms. Without any mutation, there is low probability of improvement. Mutating will change the bias or weights in neural networks, changing the output of the neural network. It can have a positive, but also a negative effect on the outcome of the neural network. However, one of the [guidelines](https://en.wikipedia.org/wiki/Genetic_algorithm#Selection) of genetic algorithms is too make sure that only the positive effects will be carried on.
### Methods
At the moment, there are 7 built-in mutation methods (all for networks):
Name | Action |
---- | ------ |
ADD_NODE | Adds a node
SUB_NODE | Removes node
ADD_CONN | Adds a connection between two nodes
SUB_CONN | Removes a connection between two nodes
MOD_WEIGHT | Modifies the weight of a connection
MOD_BIAS | Modifies the bias of a node
MOD_ACTIVATION | Modifies the activation function of a node
ADD_SELF_CONN | Adds a self-connection to a node
SUB_SELF_CONN | Removes a self-connection from a node
ADD_GATE | Makes a node gate a connection
SUB_GATE | Removes a gate from a connection
ADD_BACK_CONN | Adds a recurrent connection
SUB_BACK_CONN | Removes a recurrent connection
SWAP_NODES | Swaps the bias and squash function between two nodes
### Usage
All of these mutation functions can be executed on any kind of network:
```javascript
myNetwork.mutate(methods.mutation.<MUTATION_METHOD>);
// eg.
myNetwork.mutate(methods.mutation.ADD_NODE);
```
And some on them on nodes (`MOD_BIAS` and `MOD_ACTIVATION`):
```javascript
myNode.mutate(methods.mutation.<MUTATION_METHOD>);
// eg.
myNode.mutate(methods.mutation.MOD_BIAS);
```
For `network.evolve()` and `neat()` options, specify a list of mutation methods as follows in the options (example):
```js
network.evolve(trainingset, {
mutation: [methods.mutation.MOD_BIAS, methods.mutation.ADD_NODE]
}
```
You can also specify groups of methods:
```js
network.evolve(trainingset, {
mutation: methods.mutation.ALL // all mutation methods
}
network.evolve(trainingset, {
mutation: methods.mutation.FFW// all feedforward mutation methods
}
```
# Config
Some methods are configurable! You can change these config values as follows:
```js
option = value;
// eg.
methods.mutation.MOD_ACTIVATION.mutateOutput = false;
```
Or you can edit the `methods/mutation.js` file to change the default values.
&zwnj;
```js
methods.mutation.SUB_NODE.keep_gates // default: true
```
When removing a node, you remove the connections and initialize new ones. Setting this option to true will make sure if the removed connections were gated, so will the new ones be.
&zwnj;
```js
methods.mutation.MOD_WEIGHT.min // default: -1
methods.mutation.MOD_WEIGHT.max // default: 1
```
Sets the upper and lower bounds of the modification of connection weights.
&zwnj;
```js
methods.mutation.MOD_BIAS.min // default: -1
methods.mutation.MOD_BIAS.max // default: 1
```
Sets the upper and lower bounds of the modification of neuron biases.
&zwnj;
```js
methods.mutation.MOD_ACTIVATION.mutateOutput // default: true
methods.mutation.SWAP_NODES.mutateOutput // default: true
```
Disable this option if you want the have the activation function of the output neurons unchanged. Useful if you want to keep the output of your neural network normalized.
&zwnj;
```js
methods.mutation.MOD_ACTIVATION.allowed
// default:
[
activation.LOGISTIC,
activation.TANH,
activation.RELU,
activation.IDENTITY,
activation.STEP,
activation.SOFTSIGN,
activation.SINUSOID,
activation.GAUSSIAN,
activation.BENT_IDENTITY,
activation.BIPOLAR,
activation.BIPOLAR_SIGMOID,
activation.HARD_TANH,
activation.ABSOLUTE
]
```
This option allows you to specify which [activation functions](activation.md) you want to allow in your neural network.
&zwnj;

76
node_modules/neataptic/mkdocs/templates/docs/methods/rate.md generated vendored Normal file
View File

@@ -0,0 +1,76 @@
description: A list of rate policies that can be used during the training of neural networks.
authors: Thomas Wagenaar
keywords: learning rate, policy, exponential, step, neural-network
Rate policies allow the rate to be dynamic during the training of neural networks.
A few rate policies have been built-in, but it is very easy to create your own
as well. A detailed description of each rate policy is given below.
You can enable a rate policy during training like this:
```javascript
network.train(trainingSet, {
rate: 0.3,
ratePolicy: methods.rate.METHOD(options),
});
```
#### methods.rate.FIXED
The default rate policy. Using this policy will make your rate static (it won't
change). You do not have to specify this rate policy during training per se.
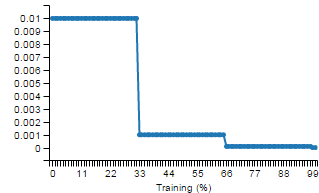
#### methods.rate.STEP
The rate will 'step down' every `n` iterations.
![step down rate](https://i.gyazo.com/4096f7093153d3512b28c35719aef688.png)
The main usage of this policy is:
```javascript
methods.rate.STEP(gamma, stepSize)
// default gamma: 0.9
// default stepSize: 100
```
A gamma of `0.9` means that every `stepSize` iterations, your current rate will
be reduced by 10%.
#### methods.rate.EXP
The rate will exponentially decrease.
![exponential decrease](http://systems-sciences.uni-graz.at/etextbook/assets/img/img_sw2/decline.JPG)
The main usage of this policy is:
```javascript
methods.rate.EXP(gamma)
// default gamma: 0.999
```
The rate at a certain iteration is calculated as:
```javascript
rate = baseRate * Math.pow(gamma, iteration)
```
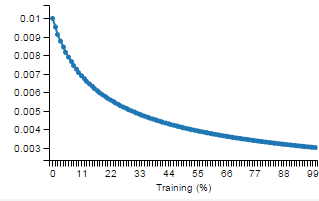
So a gamma of `0.999` will decrease the current rate by 0.1% every iteration
#### methods.rate.INV
![reverse decay](https://i.gyazo.com/7c7a1d76f1cf3d565e20cc9b44c899a8.png)
The main usage of this policy is:
```javascript
methods.rate.INV(gamma, power)
// default gamma: 0.001
// default power: 2
```
The rate at a certain iteration is calculated as:
```javascript
rate = baseRate * Math.pow(1 + gamma * iteration, -power)
```

54
node_modules/neataptic/mkdocs/templates/docs/methods/regularization.md generated vendored Normal file
View File

@@ -0,0 +1,54 @@
description: List of regularization methods in Neataptic
authors: Thomas Wagenaar
keywords: regularization, dropout, neural-network, training, backpropagation, momentum
Regularization helps to keep weights and/or biases small in your network. Some
regularization methods also make sure that you are not overfitting your data.
### Dropout
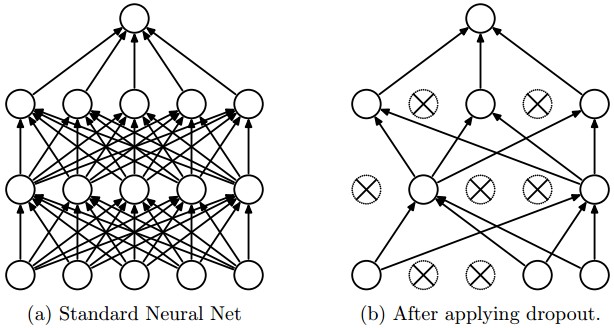
Enabling dropout will randomly set the activation of a neuron in a network to `0`
with a given probability.
![](http://cs231n.github.io/assets/nn2/dropout.jpeg)
Only use dropout when you are working with large datasets that may show some noise.
Dropout is a method that prevents overfitting, but it shouldn't work on datasets
like XOR or SINUS, as they don't have any noise. Dropout can only be used during
training:
```javascript
myNetwork.train(myTrainingSet, {
error: 0.03,
iterations: 1000,
rate: 0.3,
dropout: 0.4 // if you're not sure, use 0.5
});
```
Setting the dropout to `0.4` means that 40% of the neurons will be dropped out
every training iteration. Please note that Neataptic has no layered network
architecture, so dropout applies to the complete hidden area.
### Momentum
Momentum simply adds a fraction m of the previous weight update to the current one.
When the gradient keeps pointing in the same direction, this will increase the size
of the steps taken towards the minimum. It is therefore often necessary to reduce
the global learning rate µ when using a lot of momentum (m close to 1).
If you combine a high learning rate with a lot of momentum, you will rush past the
minimum with huge steps! Read more about it [here](https://www.willamette.edu/~gorr/classes/cs449/momrate.html).
![Momentum weight update equation](https://www.willamette.edu/~gorr/classes/cs449/equations/momentum.gif)
you can use this option during training:
```javascript
myNetwork.train(myTrainingSet, {
error: 0.03,
iterations: 1000,
rate: 0.3,
momentum: 0.9
});
```
Setting the momentum to `0.9` will mean that 90% of the previous weight change
will be included in the current weight change.

78
node_modules/neataptic/mkdocs/templates/docs/methods/selection.md generated vendored Normal file
View File

@@ -0,0 +1,78 @@
description: List of selection methods in Neataptic
authors: Thomas Wagenaar
keywords: genetic-algorithm, fitness, elitism, selection
[Selection](https://en.wikipedia.org/wiki/Selection_(genetic_algorithm)) is the
way in which a genetic algorithm decides which neural networks will be parents
for the new generation. There are a couple of selection methods, however only a
few have been integrated until now.
At the moment, there are 3 built-in selection methods:
Name |
---- |
selection.POWER |
selection.FITNESS_PROPORTIONATE |
selection.TOURNAMENT |
_A description on how each of these work is given below_
### Usage
You can specify your selection method while calling the `evolve()` function on a
network or when constructing a new instance of the `NEAT` algorithm:
```javascript
var myNetwork = new architect.Perceptron(1,1,1);
var myTrainingSet = [{ input:[0], output:[1]}, { input:[1], output:[0]}];
myNetwork.evolve(myTrainingSet, {
generations: 10,
selection: methods.selection.POWER // eg.
});
```
Next to selection methods, `elitism` is also built in the `NEAT` constructor.
[Elitism](https://en.wikipedia.org/wiki/Genetic_algorithm#Elitism) allows a
genetic algorithm to pass on `n` neural networks with the highest fitness from
the previous generation to the new generation, without any crossover steps in
between. At the moment, elitism is only possible inside a `Neat` object. They
can be passed on as follows:
```javascript
var evolution = new Neat({
selection: methods.selection.FITNESS_PROPORTIONATE,
elitism: 5 // amount of neural networks to keep from generation to generation
});
```
#### methods.selection.POWER
When using this selection method, a random decimal value between 0 and 1 will
be generated. E.g. `0.5`, then this value will get an exponential value, the
default power is `4`. So `0.5**4 = 0.0625`. This will be converted into an index
for the array of the current population, which is sorted from fittest to worst.
**Config:**
* _methods.selection.POWER.power_ : default is `4`. Increasing this value will
increase the chance fitter genomes are chosen.
#### methods.selection.FITNESS_PROPORTIONATE
This selection method will select genomes with a probability proportionate to their fitness:
![Formula](https://wikimedia.org/api/rest_v1/media/math/render/svg/89d0cb75150cdb5ad94ba7b168f217f9c290ee09)
Read more about roulette selection [here](https://en.wikipedia.org/wiki/Fitness_proportionate_selection).
#### methods.selection.TOURNAMENT
This selection method will select a group of genomes from the population randomly,
sort them by score, and choose the fittest individual with probability `p`, the
second fittest with probability `p*(1-p)`, the third fittest with probability
`p*((1-p)^2)`and so on. Read more [here](https://en.wikipedia.org/wiki/Tournament_selection).
**Config:**
* _methods.selection.TOURNAMENT.size_ : default is `5`. Must always be lower than
the population size. A higher value will result in a population that has more
equal, but fitter, parents.
* _methods.selection.TOURNAMENT.probability_ : default is `0.5`. See the
explanation above on how it is implemented.