sakuya/node_modules/neataptic/mkdocs/templates/docs/methods/rate.md

description: A list of rate policies that can be used during the training of neural networks.
authors: Thomas Wagenaar
keywords: learning rate, policy, exponential, step, neural-network

Rate policies allow the rate to be dynamic during the training of neural networks.
A few rate policies have been built-in, but it is very easy to create your own
as well. A detailed description of each rate policy is given below.

You can enable a rate policy during training like this:

```javascript
network.train(trainingSet, {
  rate: 0.3,
  ratePolicy: methods.rate.METHOD(options),
});
```

#### methods.rate.FIXED
The default rate policy. Using this policy will make your rate static (it won't
change). You do not have to specify this rate policy during training per se.

#### methods.rate.STEP
The rate will 'step down' every `n` iterations.

![step down rate](https://i.gyazo.com/4096f7093153d3512b28c35719aef688.png)

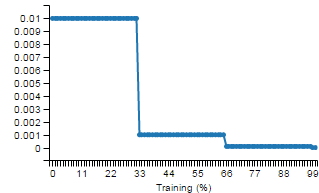
The main usage of this policy is:

```javascript
methods.rate.STEP(gamma, stepSize)

// default gamma: 0.9
// default stepSize: 100
```

A gamma of `0.9` means that every `stepSize` iterations, your current rate will
be reduced by 10%.

#### methods.rate.EXP
The rate will exponentially decrease.

![exponential decrease](http://systems-sciences.uni-graz.at/etextbook/assets/img/img_sw2/decline.JPG)

The main usage of this policy is:

```javascript
methods.rate.EXP(gamma)

// default gamma: 0.999
```

The rate at a certain iteration is calculated as:

```javascript
rate = baseRate * Math.pow(gamma, iteration)
```

So a gamma of `0.999` will decrease the current rate by 0.1% every iteration

#### methods.rate.INV
![reverse decay](https://i.gyazo.com/7c7a1d76f1cf3d565e20cc9b44c899a8.png)

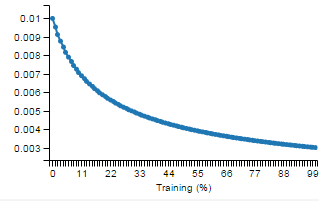
The main usage of this policy is:

```javascript
methods.rate.INV(gamma, power)

// default gamma: 0.001
// default power: 2
```

The rate at a certain iteration is calculated as:

```javascript
rate = baseRate * Math.pow(1 + gamma * iteration, -power)
```